이전 포스팅에서는 DCF method를 공부하기 위해 NPV와 FCF의 개념에 대해서 알아보았습니다.
“ 잉여현금흐름(FCF)을 가중평균자본비용(WACC)으로 할인하여 현재 시점의 가치로 환산한 순현재가치(NPV)를 우리는 ‘기업가치’라고 부르며, 이를 통해 ‘주식 가치’를 산정할 수 있게 됩니다. “
“잉여현금흐름은 영업활동으로 인한 현금흐름에서 재투자/제반 비용을 제외한 것으로 투자자들 혹은 채권자들에게 사용될 수 있는 모든 현금을 뜻합니다. “
” 잉여현금흐름(FCF) = FCF = EBIT (1-t) + DEP (Depreciation) – △WC – Investment(=Capex) + [ Terminal Value ] “
WACC(가중평균자본비용) 에 대해서
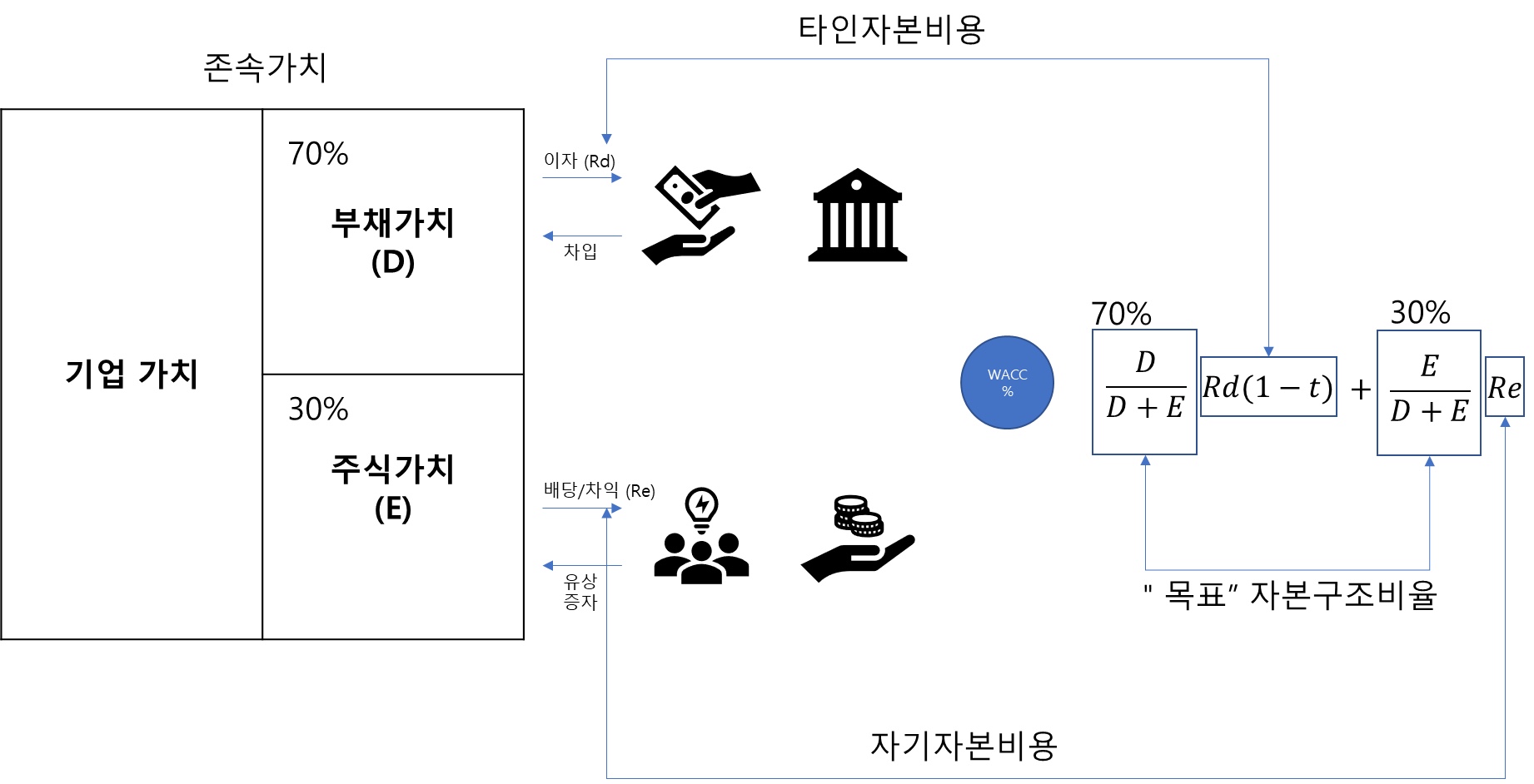
가중평균자본비용(WACC : Weighted Average Cost of Capital) 이란, 기업이 자본을 조달하는 데 드는 평균 비용을 의미합니다.
WACC는 기업이 발행한 부채와 자본의 비중에 따라 각 자본의 비용을 가중 평균하여 계산됩니다.
그렇기 때문에 가중평균자본비용을 이해하기 위해서는 타인자본비용/자기 자본비용/자본구조 비율을 이해할 필요가 있습니다.
기업 재무에서의 자본비용 (Cost of Capital)이란 주주들이 기대하는 수익률을 의미합니다. 주주들은 주식에 투자할 때 특정 수익률을 기대하며, 이 기대 수익률이 자본 비용으로 계산됩니다.
쉽게 말해, 은행의 입장에서는 부채 또는 채무 가치에 대한 이자 수익률이며 투자자에게는 투자 금액에 대한 요구 수익률이라고 할 수 있습니다.
이전에도 설명한 것처럼 기업 재무에서 은행/투자자는 각 각 이자와 배당/차익의 형태로 수익을 요구하고 있습니다.
이처럼 WACC는 채권자 및 투자자 입장에서의 평균요구수익률(이자/배당/차익 수익률)을 의미하며, 기업 입장에서는 사업에서 벌어들여야 하는 최소 수익률을 의미하게 됩니다.
타인자본비용
타인자본비용(Rd : Required Rate of Return on Debt) 또는 부채 비용은 기업이 부채를 조달하는 데 드는 비용을 의미합니다.
이는 은행과 같은 채권자의 입장에서 차입금 또는 회사채에 대한 이자율로 측정됩니다.
기업 입장에서는 조달자금에 대해 지급해야 하는 이자와 같은 대가이며, 이를 Kd (Cost of Debt)라고 하기도 합니다.
자기자본비용
자기자본비용(Re : Required Rate of Return on Equity) 또는 자본 비용은 주주들이 기대하는 수익률을 의미합니다.
기업 입장에서는 조달받은 자금에 대한 배당 혹은 시세차익과 같은 대가이며, 이를 Ke (Cost of Equity)라고 하기도 합니다.
일반적으로는 타인자본비용(Rd)이 자기자본비용(Re)보다 저렴합니다. 이를 다르게 말한다면 채권자가 요구하는 수익률이 주주가 요구사하는 수익률보다 낮습니다.
* 금융 자산의 risk와 요구 수익률은 양의 상관관계를 갖고 있습니다.
이는 다음과 같이 채권자가 부담하는 위험보다 주주가 부담하는 위험이 더 크기 때문에 발생하는 현상입니다.
예를 들면, 손익계산서 상에서 채권자인 은행에게 이자를 먼저 지급하고 세금을 납부한 후 주주에게 배당을 지급하게 됩니다.
또한 파산을 했을 경우, 채권자가 주주보다 잔여재산분배에 대한 우선순위를 갖습니다.
자본구조비율
가중평균자본비용(WACC)을 구할 때 사용하는 자본구조비율은 ‘장부가치’가 아닌 ‘존속가치’를 기준으로 합니다.
즉, 자본구조비율 (자본비중/부채비중) 을 구할 경우 총 자본 혹은 부채의 기업 가치를 총 자본으로 나누어서 구하게 됩니다.
그러나 WACC를 구하는 가장 큰 이유는 주식 가치를 구하기 위함이니 모순적인 상황이 발생하게 됩니다.
기업 가치를 구해야 하는데 필요한 WACC를 구하기 위해서 자본/부채 가치가 필요하다는 것은 말이 되지 않습니다.
따라서 이를 회피하기 위해 자본구조비율은 기업이 장기적으로 지향하는 존속가치 기준의 “목표“자본구조비율 (업좀평균부채비율 등)을 사용하게 됩니다.
WACC의 계산식
WACC는 하기와 같은 계산식으로 계산하게 되는 것이 일반적입니다.
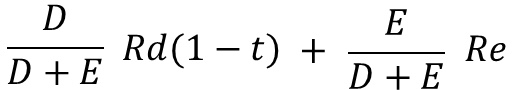
타인자본비용의 활용 – Tax Shield
기업 입장에서 타인자본비용(Rd)이 자기자본비용(Re)보다 저렴한 이유를 채권자가 부담하는 위험이 더 적기 때문이라고 위에서 서술하였습니다만, 한 가지 이유가 더 존재합니다.
이를 이자비용 절세효과 (Tax Shield)라고 하는데, 타인자본을 사용하게 되면 이자비용이 법인세를 줄여 주기 때문에 투자자에게 귀속되는 잉여현금흐름 (FCF)를 증가시켜 주는 역할을 하게 됩니다.
이처럼 타인자본비용은 자본비용의 감소 효과 그리고 FCF의 증가 효과로 각 활용하게 됩니다.
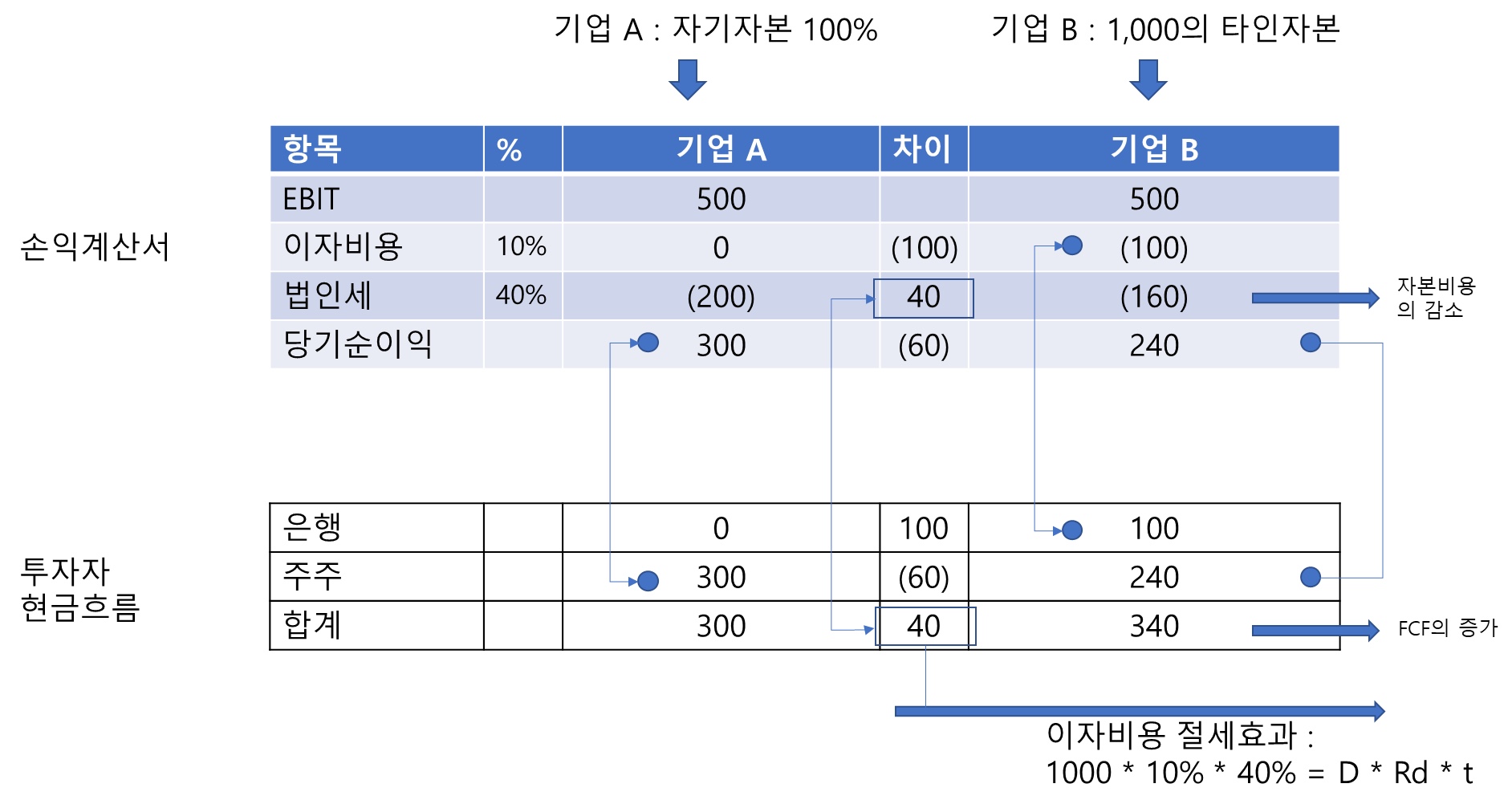
EBIT이 500으로 같으나, 자본구조가 상이한 A, B 두 기업이 있다고 가정해봅니다.
기업 A는 모두 자기 자본으로 자금을 조달하여 설립하였으며
법인세 40%로 200을 납부하였으며, 당기순이익 300은 주주의 배당재원이 되었습니다.
기업 B는 1000의 타인자본을 조달하고 나머지는 자기자본으로 조달하여 설립되었습니다.
EBIT 500에서 이자비용이 먼저 차감된 상태로 법인세는 40%인 160을 납부하였으며, 당기순이익 240은 주주의 배당재원이 되었습니다.
자본비용의 감소
자본비용의 관점에서 보게 되면, 타인자본 1000이 이자비용을 발생시켜 법인세를 40만큼 감소시켜줍니다.
따라서, 실질 이자비용은 60으로 이는 타인자본을 사용함에 따라 자본비용이 -Rd * t 만큼 감소하였다고 보는 것입니다.
FCF의 증가
한편, 잉여현금흐름(FCF) 관점에서 보면, 타인자본 1000은 은행 및 주주와 같은 투자자에게 귀속되는 이자비용과 당기순이익을 300에서 340으로 증가시켰습니다.
이에 따라 타인자본을 사용한 경우, 잉여현금흐름(FCF)이 + D * Rd * t 만큼 증가 하였다고 보게 되는 것입니다.
| 관점 | 구분 | 자본비용감소 | 잉여현금흐름(FCF) 의 증가 | ||
| 잉여현금흐름 (FCF) | EBIT (1-t) | EBIT (1-t) | 300 | EBIT (1-t) | 300 |
| Tax Shield | + D * Rd * t | 40 | |||
| EBIT (1-t) | 300 | EBIT (1-t) + D * Rd * t | 340 | ||
| 가중평균자본비용(WACC) | Rd | Rd | 10% | Rd | 10% |
| Tax Shield | – Rd * t | -4% | |||
| Rd * (1-t) | 6% | Rd | 10% | ||
Tax Shield의 활용
일반적으로 기업 재무에서는 이자비용 절세효과 (Tax Shield)를 ‘자본비용의 감소’ 관점으로 봅니다.
Tax shield는 부채 사용의 이점을 강조하며, 이는 WACC(가중평균자본비용)를 낮추는 데 기여할 수 있습니다.
부채 비중이 높아질수록 세금 절감 효과가 커지기 때문에, 이는 기업의 자본 비용을 줄이는 요인이 됩니다.
따라서 순현재가치 (NPV)를 구할 때, 자본구조와 무관하게 다음의 계산식을 활용하게 됩니다.
FCF = EBIT (1-t) + DEP (Depreciation) – △WC + [ Terminal Value ]
WACC = [ D ÷ (D+E)] * Rd(1-t) + [E ÷ (D+E) ] *Re
한편, 이자비용 절세효과를 ‘잉여현금흐름 (FCF)의 증가’ 관점에서 보게 되는 경우가 종종 존재하는데, 부채 사용 기업가치 (VL) 를 무부채 기업가치(VU) 를 통해 구하는 경우에 활용할 수 있습니다.
무부채기업가치인 (VU)를 잉여현금흐름에서 자기자본비용으로 할인하여 구합니다.
이후 부채사용기업의 잉여현금흐름은 무부채기업보다 D*Rd*t 만큼 영구적으로 많기 때문에, 이를 고든의 제로성장모형을 통해 현재가치로 환산하게 되면 부채사용 기업가치 (VL)과 무부채사용 기업가치 (VU)의 관계를 다음과 같이 도출할 수 있습니다.
VL=VU + D*Rd*t ÷ Rd = VU + D*t
자기자본비용의 활용
위에 설명한 타인자본비용 (Rd)는 은행과 같은 채권자 입장의 요구 수익률입니다.
차입금의 이자율이나 회사채의 만기수익률 등으로 이러한 요구 수익률은 명확하게 파악할 수 있습니다.
하지만, 자기자본비용 (Re)의 경우는 주주가 기대하는 수익률을 의미합니다. 따라서 주주마다 요구하는 수익률이 상이합니다.
결론적으로 자기자본비용(Re)는 이론적 모형을 통해 추정하게 됩니다.
자기자본비용 모델 – CAPM
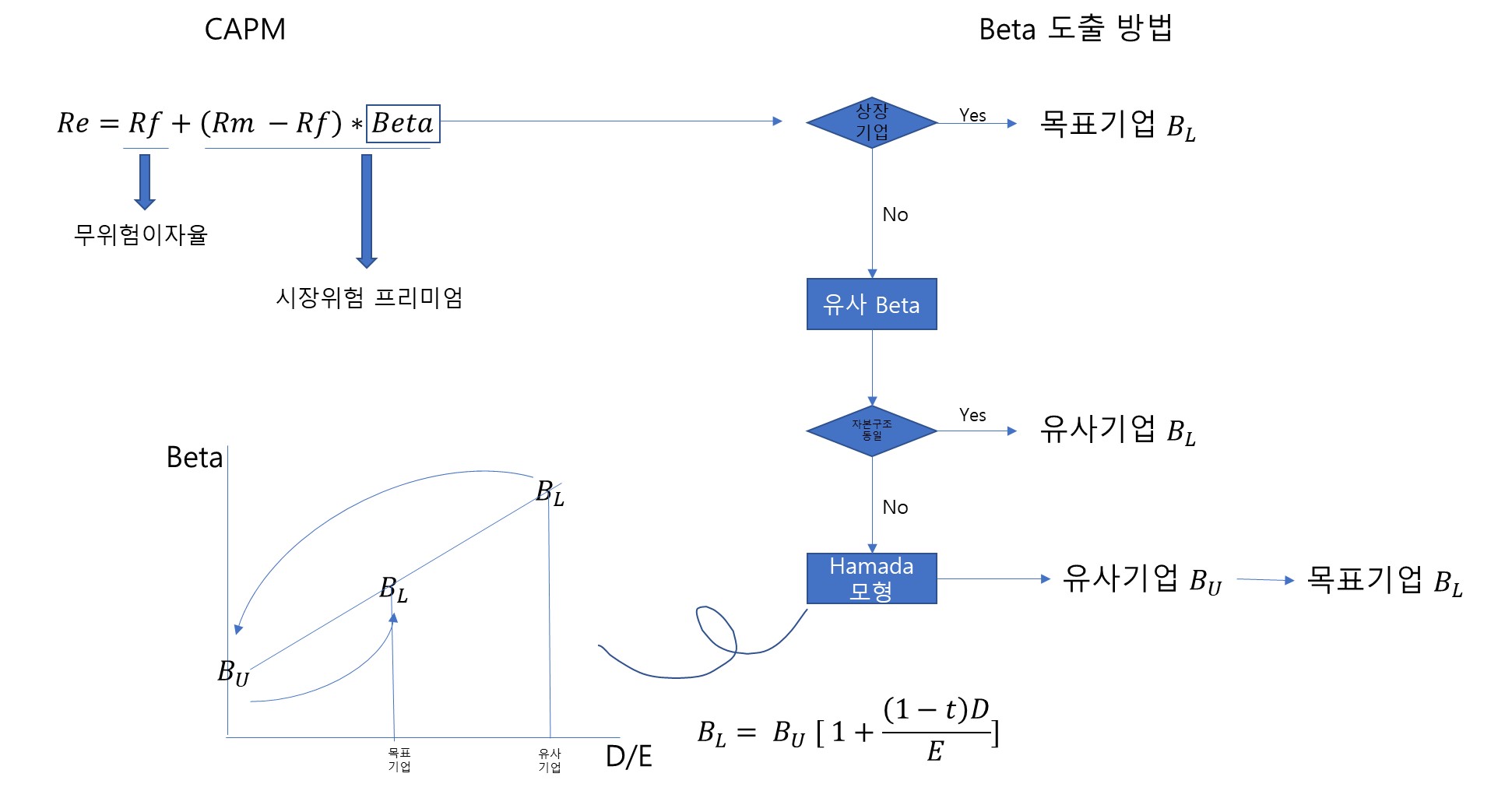
자본자산가격결정모형 (CAPM : Caplital Asset Pricing Model)이란, 자기자본비용(Re)를 추정하는 데에 가장 일반적으로 쓰이는 모형으로, 주식을 비롯한 자본자산의 위험과 기대수익률 간의 관계를 설명하는 모델입니다.
CAPM은 주주가 요구하는 최소 요구 수익률을 추정하는 방법으로 무위험 이자율과 시장위험 프리미엄 2가지의 합으로 추정할 수 있습니다.
무위험 이자율과 시장위험 프리미엄을 구하기 위해서는 Rf, Rm, Beta에 대해서 알아야 합니다.
- 무위험이자율 (Rf) : 최소한 받아야 하는 수익률을 의미합니다.
일반적으로 중간에 이자를 지급하지 않는 순수할인채인 10년 만기 장기 국채 이자율을 사용합니다. - 시장위험프리미엄 : 무위험 이자율을 초과하는 시장수익률에 개별 민감도(Beta)를 반영한 수익률입니다.
(Rm – Rf) * Beta - RM 은 시장 포트폴리오의 기대수익률입니다.
증권시장에 상장된 모든 주식의 평균 수익률로, 평가하고자 하는 기업 또는 사업의 지속성과 무관하게 충분하게 긴 종합주가지수의 평균 수익률을 사용합니다. - Beta는 시장 포트폴리오의 기대수익률과 목표 주식의 요구수익률과의 관계로, 종합주가지수가 1% 변동할 때, 목표 기업의 주식가치는 몇 % 변동되는지를 나타내는 민감도입니다.
Beta를 도출해야 할때는 먼저 상장기업의 경우 목표 기업의 Beta 정보를 시장에서 파악하여 그대로 사용할 수 있습니다.
비상장 기업의 경우에는 동종업종의 상장된 유사 기업의 Beta를 사용할 수 있습니다.
유사기업의 자본구조가 목표기업의 목표자본구조와 동일한 경우, 유사기업의 Beta를 그대로 사용할 수 있으며, 자본 구조가 상이한 경우 Hamada 모형을 통해 재무 위험을 조정한 후 Beta를 구하게 됩니다.
자기자본비용 – Hamada
위에 서술한 것처럼 CAPM 모형을 산출하기 위한 Beta를 설정하기 위해서는 Hamada모형을 이용해야 한다고 설명하였습니다.
비상장기업의 Beta는 동종업종의 상장된 유사기업들의 의미 있는 Beta를 평균화하여 사용하지만, 모든 기업의 자본구조는 상이하기 때문에 추가적으로 Beta를 조정하여 사용합니다.
이를 이해하기 위해서 Beta의 구성과 종류를 이해하는 시간을 갖도록 하겠습니다.
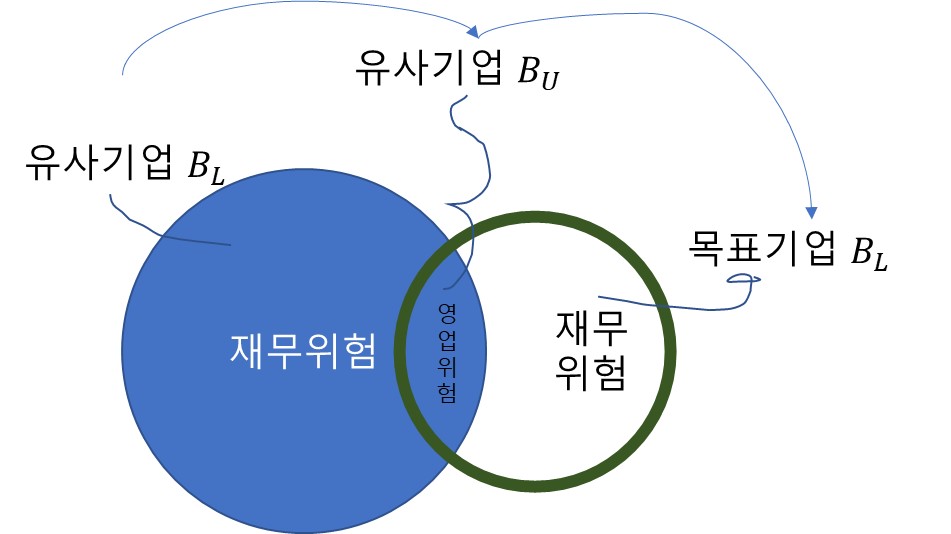
Beta는 기업의 자본구조에 따른 재무위험과 그 기업이 속한 업종의 영업위험의 합계로 구성됩니다.
따라서, 타인자본을 사용할 수록 재무위험이 증가하므로 Beta도 증가하게 됩니다.
재무위험은 타인자본의 조달에 따른 이익의 변동성을 의미합니다.
이익이 났을 때만 배당을 지급하는 자기자본과는 다르게, 타인자본은 고정적으로 이자를 지급해야만 합니다.
즉, 자기 자본 조달로 인한 배당금은 변동비용으로 처리되지만, 타인자본 조달로 인한 이자비용은 고정비용이라 볼 수 있습니다.
그리고 고정비용의 비중이 커질수록 이익의 변동성은 커지게 됩니다.
영업위험은 사업 자체에 따른 이익의 변동성을 의미하며, 그 업종에 속한 모든 기업들에게 동일하게 적용할 수 있습니다.
Unlevered Beta는 타인자본의 조달로 인한 재무위험을 제외한 Beta로 기업이 속한 영업위험만을 반영한 Beta로 Bu라고 표시합니다.
Levered Beta는 그 기업이 속한 업종의 영업위험뿐만 아니라 타인자본의 조달로 인한 재무위험까지 모두 반영한 Beta로 BL 이라고 표시합니다.
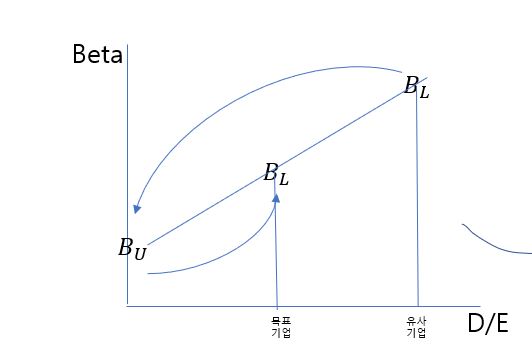
Hamada 모형은 Hamada 모형은 Modigliani-Miller 정리에서 출발하여, 기업의 자본구조가 변화할 때 베타값이 어떻게 변하는지를 보여줍니다.
공식은 Unlevered Beta와 Levered Beta간의 상관관계 등식이며, Hamada모형을 통해 다음과 같이 목표 기업의 Beta를 구할 수 있습니다.
유사기업의 Levered Beta (BL)에서 재무위험을 제거하여 그 유사기업이 속한 업종의 영엄위험만을 반영한 Unlevered Beta(Bu)를 구합니다.
영업위험만 반영한 Unlevered Beta(Bu)에 목표기업의 재무위험을 고려하여 Levered Beta(BL)을 구합니다.
예시로 기업이 속한 영업위험만을 반영한 무부채 상태의 Beta가 1.2이고, 목표 기업의 부채 비율이 50% (즉, D/E=0.5)이며, 법인세율이 30%라고 가정해보겠습니다.
Hamada 모형을 적용하여 목표기업의 Levered Beta를 계산하면 다음과 같습니다:
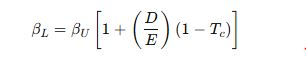
βL=1.2[1+(0.5)(1−0.3)]
βL=1.2[1+0.35]
βL=1.2×1.35=1.62
따라서, 목표기업의 Levered Beta는 1.62가 됩니다.
WACC 활용하기
한 투자자가 어느 비상장기업의 WACC를 동종업종의 상장된 유사기업의 정보를 참조하여 구하고자 한다고 가정해봅니다.
기업 A의 경우는, 목표 기업의 목표자본구조가 유사기업의 자본구조와 동일하며, 기업 B의 경우는 그 자본구조가 상이합니다. 그 이외의 조건들은 A와 B가 모두 동일합니다.
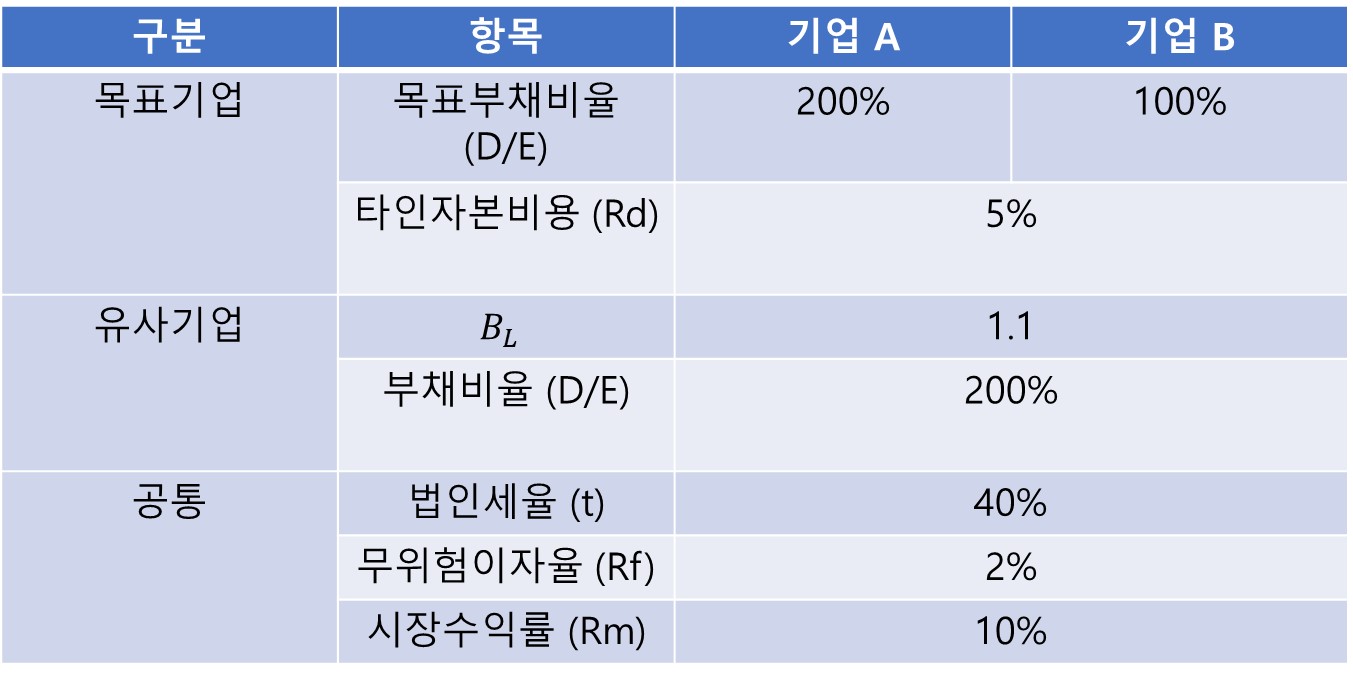
기업 A와 B의 WACC는 유사기업의 BU > 목표기업의 BL > RE > WACC 순으로 도출되게 되며 식은 하기와 같습니다.
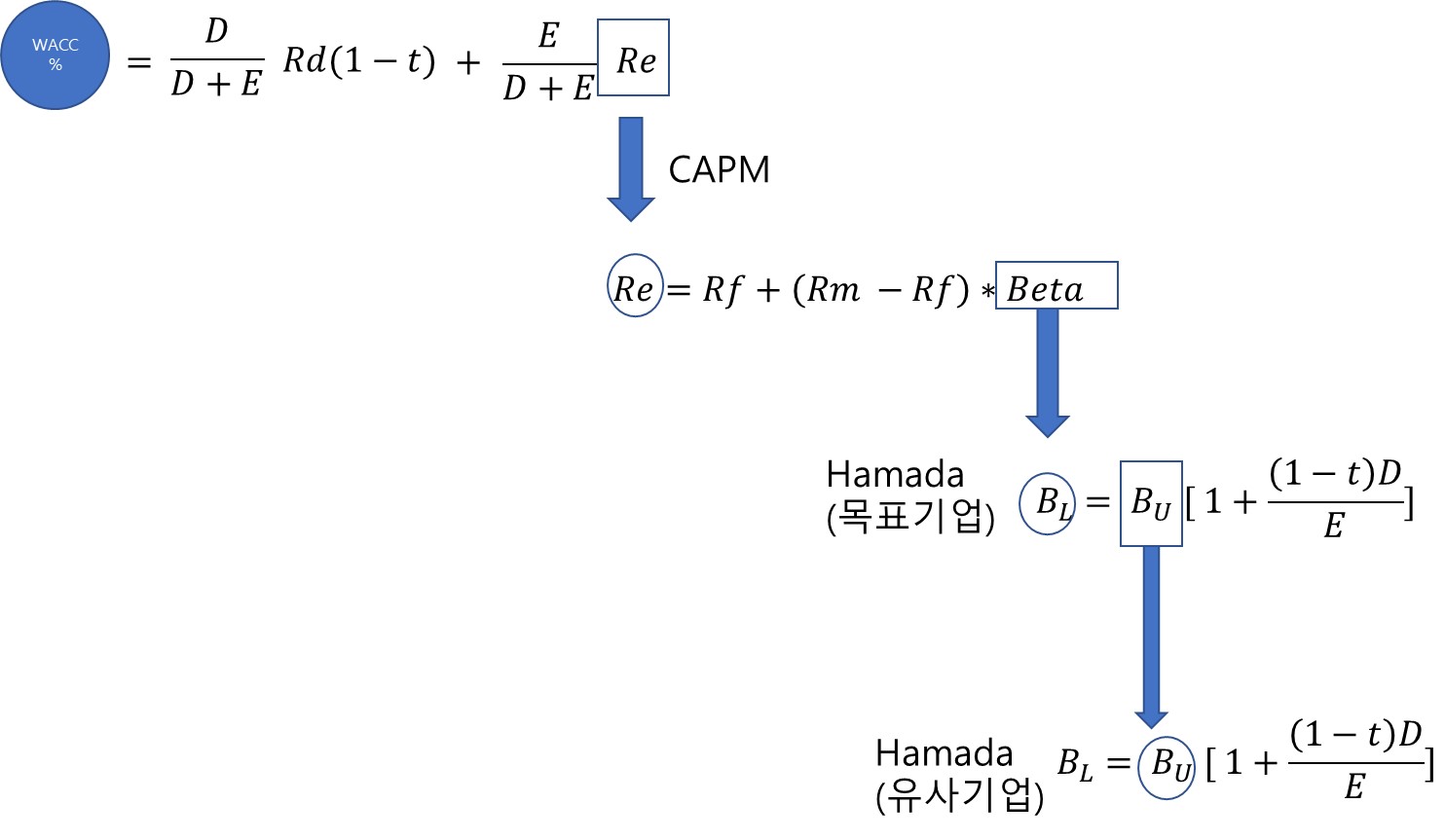

기업 A의 경우는 목표기업의 목표자본구조와 유사기업의 자본구조가 동일하여, 1단계와 2단계는 생략하고 유사기업의 Levered Beta를 그대로 사용하게 됩니다.
목표 기업의 Levered Beta를 그대로 이용하여 Re를 도출하고 이를 이용해 WACC를 구할 경우 5.6%가 나옵니다.
기업 B의 경우는 목표기업의 목표자본구조가 유사기업의 자본구조와 상이하기에, 1단계에서 재무위험을 제거하여 해당 업종 내의 영업위험만 존재하는 Unleverd Beta를 도출하고, 유사기업의 Unlevered Beta를 바탕으로 목표 기업의 재무위험을 고려한 Levered Beta를 도출하게 됩니다.
이를 이용해 CAPM을 이용하여 Re를 추정하고 WACC를 구할 경우 5.7%가 나오게 됩니다.
위 사례에서 살펴본 것 처럼 목표부채비율이 높은 기업 A가 기업 B보다 Unlevered Beta 및 Re가 높게 나타는 반면, WACC는 저렴한 Rd와 이자비용 절세효과 (Tax Sheild)로 인해 기업 A가 기업 B보다 낮게 나타나게 됩니다.
참고
본 포스팅에 이전 포스팅이 궁금하다면 하기 링크를 참고 바랍니다.
주식 가치 평가 (Valuation) _현금 흐름 할인법 (DCF Method) 1탄 : NPV
주식 가치 평가 (Valuation) _현금 흐름 할인법 (DCF Method) 2탄 : FCF
본 포스팅은 “책 MBA 회계와 기업재무, 조병헌 지음” 를 참고하여 작성되었습니다.
원작자님의 책으로 많은 공부가 되었습니다. 깊은 감사의 말씀 드립니다.
책 구매 링크가 필요하신 분은 하기 참고 바랍니다.
YES 24 : MBA 회계와 기업 재무 구매하기
교보문고 : MBA 회계와 기업 재무 구매하기
